Activity 5: Enhancement by Histogram Manipulation

Grayscaled images may look too boring since they do not possess vibrant colors, instead, they have these dull white,gray and black color. But who knew that they can be very interesting when they are manipulated in such a way that it gives effect to the image? And these manipulations are only limited to the imagination of the editor.

Histogram manipulation, the technique used to manipulate a grayscaled image to editor's will. This technique changes the image by changing the Cumulative Distribution Function (CDF) of an image. In doing so, the histogram values of the images also change and consequently the pixel values of the image changes. To elaborate this technique further, a histogram, also known as the Probability Distribution Function (PDF), displays the occurrence of different gray levels in an image matrix and by summing the area under the histogram gives the CDF of our grayscaled image. With the CDF of the image on our grasp, we can now manipulate it and change it to our desired CDF, and while doing so, since CDF is the area under the histogram curve, the PDF of the image is changed and the occurrence of gray values consequently changes.

Figure 1 shows a step-by-step method in changing or mapping the original gray levels to the new (desired) gray levels.

Figure 1. A four step method used in mapping the original gray levels to a new one defined by the desired CDF. (1) Find a specific gray level value and (2) find its corresponding original CDF value. (3) Find the CDF value on the deisred CDF and (4) find the corresponding gray level. This image is taken from the manual of Activity 5: Enhancement by Histogram Manipulation, prepared by Dr. Soriano.

Now let's go to the exciting part, manipulating the image and giving it an extra kick by mapping it to our desired CDF. Our image guinea pig is shown in figure 2, an image of a Pokemon named Charmander that was taken from Deviantart.

Figure 2. Image of Charmander, a fire-type starter from Pokemon Generation I. It evolves into Charmeleon at level 16 and finally evolves into Charizard at level 36.

Now to manipulate this true color image and get its PDF and CDF plots, we first need to get its grayscaled version. Figure 3 shows the grayscaled image and its corresponding PDF and CDF.

Figure 3. Grayscaled image and corresponding PDF and CDF of the guinea pig image in figure 2. Both PDF and CDF are normalized by the total number of pixels in the image.

Now that we have the grayscaled image and its corresponding PDF and CDF, we can now do our magic in manipulating the grayscaled image. The only thing missing now is what CDF we are going to use. Starting at a basic and less complicated CDF, we will first use a linear CDF shown in figure 4.

Figure 4. A linear CDF with a positive slope. This CDF is where we will map our original CDF.

Applying the steps mentioned above in mapping the original gray levels to the new ones, we would get an image with corresponding PDF and CDF plots shown in figure 5.

Figure 5. An image, with its corresponding PDF and CDF plots, mapped onto a linear CDF with a positive slope.

In figure 5, we see that the image somehow brightened compared to the original grayscaled image. This lightening of the image can be seen at PDF plot, we can see that there is an increase in occurrence of the higher gray values, and high values corresponds to white in gray level. Observing the new CDF of the mapped image, we can see that it is almost similar to our desired CDF, the only difference is there is a bulge on the beginning of the CDF, this bulge corresponds to high occurrence of pixels having a value of less than 50.

Adding a little tweak on the basic linear CDF, we now want to see what would the image be if the slope was changed to a negative value. So now, our desired CDF would look like this,

Figure 6. A linear CDF with a negative valued slope.

What do you think the image would look like? We can make a guess that since the slope now have a negative value, maybe something will be inverted. Let's see if we guessed right by looking at figure 7.

Figure 7. Is it really the inverse of the image found in figure 6? How about the PDF and CDF? Are they also the inverse of the PDF and CDF found in Figure 6?

Comparing the images in figures 6 and 7, we can say that the gray values of each pixels in figure 7 was inverted as compared to figure 6. Also, by looking at PDF's found in figures 6 and 7, we can see that they are just mirror images of one another. Hence we safely say that the image in figure 7 is just the invert of the image found in figure 6. But wait! How about the CDF's, they are not mirror images of each other? At first glance, we can immediately say that they are definitely not mirror images of each other, but by further examining the plot, it can be seen that the bulge observed in the beginning of the CDF in figure 6 is observed at the end of the CDF in figure 7 and both bulges in opposite direction. But still, why does the CDF in figure 7 does not have a negative slope like the CDF that was mapped onto? Well, this explains it, CDF is just the sum of the infinitesimal area under the curve of the PDF. This implies that since the infinitesimal area are positive values, the sum of these areas will yield positive values. Thus the CDF always have an increasing trend.

This gray level manipulation intrigued me, so I want to see how the image would change for specific CDF. The figures that will follow are the desired CDF, and the mapped images with its corresponding PDF and CDF.

Figure 8. CDF = exp(x).

Figure 9. CDF = exp(-x).

Figure 10. CDF = ln(x).

Figure 11. CDF = ln(k-x).

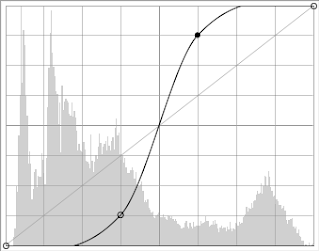
There are image editing softwares that changes the gray values by just clicking and dragging to map the original CD into a new one. An example of this software is GIMP. Gimp is free image editing software available in the internet. The interface in histogram manipulation in GIMP is so user-friendly. It got me hooked up and so I did different CDF to mapped on to.

The following images are generated through GIMP's histogram manipulator.

I found that editing images through histogram manipulation is an exciting image processing activity. It does not only gives your grayscaled image an extra kick, it also helps you understand how image editing softwares do this and that. I find this activity very interesting and thus I would proudly give myself a 10 in this activity.

*The code used in backprojecting is shown below:

for r = X // X is the gray levels of the original grayscaled image

z = func(r); // func gives the corresponding gray level value of r in the desired CDF

Image(find(Image == r)) = z; // Replaces the pixels with gray level value r with z

end

Reference:

Dr. Soriano. Applied Physics 186 activity handouts: A5 - Enhancement by Histogram Manipulation.